


Schachzwerg translates to "chess dwarf".
@author Andre Adrian
@date 2019-08-31
The chess game was once the "Drosophila melanogaster" of the
artificial intelligence (AI) research. The creator of an
AI-program is intelligent, but is the creation intelligent, too?
This is a statement from L. Torres y Quevedo, the creator of the
first chess playing machine, to a Scientific America reporter in
1915:
| There is, of course, no claim that it will
think or accomplish things where thought is necessary, but
its inventor claims that the limits within which thought is
really necessary need to be better defined, and that the
automaton can do many things that are popularly classed with
thought. It will do certain things which depend upon certain
conditions, and these according to arbitrary rules selected
in advance. |
One school of thought simply says: If it passes the Turing test,
it is intelligent. The other school of thought says: We have no
good definition of intelligence, how can we have a definition of
artificial intelligence?
What is the purpose of this endeavour? First to have fun and learn
something new. Second to verify or reject the "small is enough"
idea. Third to create the philosophical question: How can a
creator with a chess performance rating of 1000 Elo create a chess
computer with a chess performance of 1500 Elo (yes, this is the
design goal).
The predecessor of ESP Schachzwerg and Super ESP Schachzwerg is my
AVR
MAX Schachzwerg chess computer from 2009. The magazine
Elektor provided a kit. A PCB, an ATMega88V SoC
(System-on-a-Chip), some push-buttons, four 7-segment LEDs and two
AA batteries . Performance is 1290 Elo out of 8MHz 8-bit CPU,
8KByte ROM and 1KByte RAM. Because of RAM limitations a
non-recursive version of the search algorithm was used. The
program is based on Micro-Max
from H.G. Muller.
The program of ESP Schachzwerg should work like an insect brain
or a hummingbird brain: a little animal can only afford a little
brain. But because the little animal has to live in the same
complex environment as bigger animals with larger brains it can
not afford to be stupid. Scientific American MIND July/August 2017
magazine wrote: "How could such a tiny brain perform as well as a
bigger one? Through vicious, cutthroat evolutionary efficiency".
The same "small is enough" principle is used for ESP Schachzwerg.
The program uses primitive evaluation for a deep search within the
limitations of the hardware.
The typical computer for a chess program in 1974 was an IBM
360/168 mainframe. But Johann Joss used a HP2115A mini computer.
This 16-bit computer was on the market since 1967. The maximum
core memory amount was 8KWord, that is 16KByte.

Picture: The HP2115A cabinet. Another cabinet the same size
housed the power supply.
With strong competition in Stockholm 1974, Tell got rank 11 out
of 13. In Dortmund, 1975, competition was weak and Tell got first
rank! In Toronto 1977 Tell only got last rank The strong
competition at this time was Chess from U.S.A. and Kaissa from
UdSSR. This was the time of cold war at the computer chessboard.
| Rank |
1974 Stockholm |
1975 Dortmund |
1977 Toronto |
| 1 |
Kaissa |
Tell |
Chess 4.6 |
| 2 |
Chaos |
Daja |
Duchess |
| 3 |
Chess 4.0 |
Schach MV 5,6 |
Kaissa |
| 4 |
Ribbit |
Orwell III |
Belle |
| 11 |
Tell |
- |
Black Knight |
| 16 |
- |
- |
Tell |
The chess computer Belle was special. It was a PDP-10 together
with special hardware. Belle terminated the reign of the mainframe
chess dinosaurs. Orwell III was written by Nitsche. Nitsche and
Henne and the Mephisto chess computer made Hegener & Glaser an
important chess computer company.
There are CISC and RISC CPUs. And there are RISC and modern RISC
CPUs. A traditional 32-bit RISC has 32-bit opcodes. This is a
waste. Modern RISC like ARM
Thumb or Xtensa have 16-bit or 24-bit opcodes. These small
size opcodes make opcode fetch a little more complicated, but
bring RISC CPU code density quality to CISC CPU quality. Remember,
the micro-code and nano-code Motorola 68000 CISC had 16-bit
opcodes. One of the first publications about the RISC CPU that is
used in the Espressif SoCs is the 2008 Tensilica Diamond
white paper. The Xtensa ISA is documented in the 2004
Tensilica LX Microprocessor. There is a Xtensa Instruction
Set Architecture (ISA) Reference Manual available, too.
The ESP8266, ESP8285 and ESP32 SoCs from Espressif were designed
as WLAN-bridge or WLAN-modem, an IO-chip that gives another CPU
WLAN (WiFi) or Bluetooth (BLE) capabilities. That is, it was the
chinese low-cost answer to the Nordic nRF24 chips. The big
difference is that the ESP SoCs can execute user programs next to
the protocol stack firmware. The ESP8266/ESP8285 use a Tensilica
Diamond 106Micro (L106) 32-bit 80MHz CPU. The program execution is
somewhat special. The program is read from an external Flash
memory into the 32KByte execution cache/32 KByte execution memory.
A jump outside the 32KByte segment triggers a load from Flash.
This is slower than having "real" memory for program memory, but
cheap. The ESP8266/ESP8285 RAM is 80KByte. The ESP8266 has
normally 4MByte of external Flash, the ESP8285 has 1MByte internal
Flash. Price for a DOIT ESP8285 NodeMCU-M
DevKit is US$ 2.50
The user interface is done very modern with a touchscreen LCD. A
stylus is used as in the old Palm PDA handheld computers. The LCD
is of good quality TN technology with 6-bit color depth per
primary color, LED backlight and 240x320 pixel resolution.
The DevKit and the touchscreen LCD are available as ready-made
breadboard modules. The breadboard has 2.54mm (1/10 inch)
contacts. After hardware development on breadboard, a simple PCB
can replace the breadboard. I choose the NodeMCU-M ESP8285 module
that provides USB port, USB-to-UART bridge and 3.3V voltage
regulator. The touchscreen LCD has SPI interface for
LCD-controller and touch-controller. The controller chips ILI9341
for LCD and XPT2046 for touch are fully supported by the IDE.
The brightness of the LCD backlight is selected with a resistor. A
33Ω resistor is used. The ESP SoCs and other components are 3.3V
devices. Therefore a 3.6V lithium battery in AA form factor is
used. A 5V USB power supply works as well. An on/off switch,
battery holder and insulated wire completes the hardware BOM (bill
of materials).
 |
 |
 |
Top picture: DOIT NodeMCU-M DevKit with ESP-M2 module using
ESP8285 SoC.
Second picture: TJCTM24028-SPI 2.8" touchscreen LCD ILI9341,
XPT2046.
Bottom picture: 400 pins breadboard.
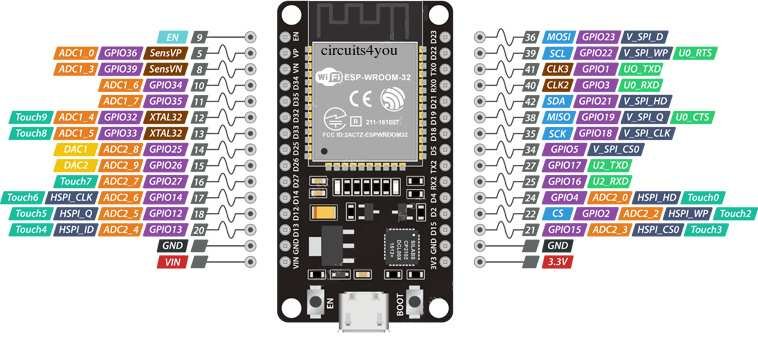
The ESP have the Flash SPI interface at GPIO 6 to 11. These GPIO
pins are best left alone. The ESP8266/ESP8285 has an additional
hardware SPI. The SPI signals Clock-Out, MISO and MOSI are
connected to ESP8266/ESP8285 pins GPIO14 (D5), GPIO12 (D6)
and GPIO13 (D7). Expressif uses the GPIO naming, DOIT NodeMCU
DevKit uses the Arduino Dx naming. These signals go to the
LCD and to the touchscreen in parallel, that is ESP Clock-Out is
connected to LCD Clock-In and Touch Clock-In. To separate the two
devices LCD and touch, every device has a Chip Select (CS) pin.
The LCD CS is connected to ESP pin GPIO15 (D8), the touch CS is
connected to GPIO4 (D2). The LCD can receive data or command
codes. The code type is transmitted via the LCD Data Command (DC)
signal which is connected to ESP GPIO5 (D1). The Reset or EN pin
of the ESP is connected to the LCD reset pin. And last but not
least, the LCD backlight pin is connented via a 33Ω resistor to
3.3V. The power supply pins 3.3V and GND are routed between ESP
and touchscreen LCD module, too. The on/off switch is
traditionally placed in the 3.3V wire between battery and circuit.
But you can also place it in the GND wire. As an old telephone
technician I could tell you why this is the correct way to do
things, but our little system has no earth connection and
therefore this information is not needed.
| ESP8266 |
ESP8285 |
ESP32 |
LCD |
Touch |
| D5 |
GPIO 14 |
GPIO 18 |
SPI CLK |
SPI T_CLK |
| D7 |
GPIO 13 | GPIO 23 |
SPI MOSI |
SPI T_DIN |
| D6 |
GPIO 12 | GPIO 19 |
SPI MISO |
SPI T_DO |
| D8 |
GPIO 15 | GPIO 15 |
LCD CS |
n/a |
| D1 |
GPIO 5 | GPIO 5 |
LCD DC |
n/a |
| D2 |
GPIO 4 | GPIO 4 |
n/a |
T_CS |
| RST |
EN |
EN |
RESET |
n/a |
The SPI bus uses serial data transfer. The ESP is the bus master.
Only the master provides the clock signal. The "Master Out Slave
In" MOSI pin is an output at the ESP and an input at the LCD or
touch. The "Master In Slave Out" operates in the other direction.
The SPI bus is really primitive, and best of all does not need
royalty payment.
The current consuption is 48mA@3.6V for the ESP8285 and 88mA@3.6V
for the ESP32 running the Mandelbrot demo program on a 2.4"
touchscreen LCD. WLAN is switched off at ESP8285, but not at
ESP32.
The ESP8266/ESP8285 can be replaced by an ESP32 module like the
DOIT ESP32
DevKit, the Espressif DevKitC V4 or clones. The
ESP32-WROOM-32 module is the slightly more expensive "bigger and
better" brother. DOIT ESP32 DevKit price is US$ 3.85. It has a
dual core Tensilica Xtensa LX6 32-bit 240MHz CPU, 160KByte static
allocated RAM, 160KByte dynamic allocated RAM and 4MByte Flash.
This amount of RAM allows a transposition table. A Super ESP
should have 1700 Elo. The Spracklens did 1755 Elo in 1983 with a
3.2MHz 8-bit 6502, 24KByte ROM and 3KByte RAM.
 |
 |
Top Picture: 30pin DOIT ESP32 DevKit with ESP-Wroom-32 module
using ESP32 SoC.
Bottom Picture: 38pin Expressif DevKitC V4 with ESP-Wroom-32
module using ESP32 SoC.
@note Espressif DevKitC V4 and clones are Arduino board "ESP32
Dev Module"
@note press the BOOT key if "Connecting ..." is displayed. Release
the key after upload starts.
The GPIO pin 0 is used for the BOOT key. The pins 1 and 3 are used
for serial monitor. Pins 6 to 11 are used for Flash memory
interface. These pins should not be used. The GPIO pins 34, 35,
36, 39 are input only. The default SPI pins are 18 for CLK, 19 for
MISO and 23 for MOSI. The difference between 30 pin and 38 pin
DevKits is small. The GPIO pins 6 to 11 are useless. The GPIO pin
0 is wired to the BOOT key. If used as a output it can create a
short circuit if the pin output is high and the key forces it low.
The last difference is one more GND pin. The 30 pin DevKit is
cheaper and more practical.

This demo program is output only, that is, it uses only the LCD.
It was used to familiarize with hardware SPI, firmware
yield() and RAM. The RAM size of the ESP32 shrank from
520KByte (DRAM+IRAM) to 320KByte (DRAM) to 160KByte static
allocated + 160KByte dynamic allocated further to 110KByte
available dynamic allocated DRAM. For me this is the difference
between optimism and realism: the transposition table size is
110KByte, not more. The same source code is for ESP8266, ESP8285
and ESP32. Just define ESP8266 for the first two or ESP32 for the
third. Define USE_BUFFER will draw the animation faster, but will
not use the full LCD area. ESP32 has 110KByte RAM for the buffer
and ESP8266/ESP8285 has 50KByte RAM for the buffer. The ESP32
program runs three times faster than the ESP8285 program. This
suggests that 106Micro in ESP8285 runs at 80MHz and LX6 in ESP32
runs at 240MHz and there are no differences in both CPUs - at
least not for this program.
| /* @file mandelbrot_ili9341 @brief Mandelbrot set animation Hardware: ESP8266/ESP8285/ESP32 + TJCTM24024-SPI/TJCTM24028-SPI LCD resolution 320x240, LCD controller ILI9341 based on Adafruit ILI9341 mandelbrot the fractal pattern is unlimited, but the numeric precision is limited @author Andre Adrian @date 2019-08-30 */ #define ESP8266 // or #define ESP32 #define USE_BUFFER // or deactivate this #define #include <Adafruit_GFX.h> // version 1.5.6 #include <Adafruit_ILI9341.h> // version 1.5.1 #ifdef ESP8266 # include <ESP8266WiFi.h> # define BITRATE 74880 #endif #ifdef ESP32 # include <WiFi.h> # define BITRATE 115200 #endif // HW SPI CLK MISO MOSI // ESP8266 D5 D6 D7 // ESP8285 14 12 13 // ESP32 18 19 23 #define TFT_CS 15 #define TFT_DC 5 // Use hardware SPI and the above for CS/DC Adafruit_ILI9341 tft = Adafruit_ILI9341(TFT_CS, TFT_DC); const int16_t bits = 28, // Fractional resolution iterations = 96; // Fractal iteration limit or 'dwell' int16_t pixelWidth = 320, // TFT dimensions pixelHeight = 240 - 1; float centerReal0 = -0.6, // Image center point in complex plane centerImag0 = 0.0, rangeReal0 = 3.0, // Image coverage in complex plane rangeImag0 = 3.0, delta0 = -0.1; #if defined(USE_BUFFER) uint16_t *buffer = NULL; #endif void setup(void) { #ifdef ESP8266 WiFi.disconnect(); WiFi.mode(WIFI_OFF); WiFi.forceSleepBegin(); yield(); #endif #ifdef ESP32 // @todo change this Espressif software to Arduino software // https://docs.espressif.com/projects/esp-idf/en/latest/api-reference/system/sleep_modes.html // esp_bluedroid_disable(); // esp_bt_controller_disable(); // https://docs.espressif.com/projects/esp-idf/en/latest/api-reference/network/esp_wifi.html // esp_wifi_stop(); // esp_wifi_set_mode(WIFI_MODE_NULL); #endif Serial.begin(BITRATE); Serial.println(); // synchronize serial monitor (less garbage output) Serial.println("Mandelbrot set animation"); tft.begin(); tft.setRotation(1); tft.fillScreen(ILI9341_BLACK); #if defined(USE_BUFFER) // https://docs.espressif.com/projects/esp-idf/en/latest/api-reference/system/mem_alloc.html // ESP32: Due to a technical limitation, the maximum statically allocated DRAM usage is 160KB. // The remaining 160KB (for a total of 320KB of DRAM) can only be allocated at runtime as heap. uint32_t size; for (;;) { size = pixelWidth * pixelHeight * sizeof(uint16_t); buffer = (uint16_t *)malloc(size); if (buffer != NULL) break; pixelWidth -= 2; pixelHeight -= 2; } Serial.print("pixelWidth="); Serial.print(pixelWidth); Serial.print(" pixelHeight="); Serial.print(pixelHeight); Serial.print(" size="); Serial.println(size); #endif } void loop() { float centerReal = centerReal0, centerImag = centerImag0, rangeReal = rangeReal0, rangeImag = rangeImag0, delta = delta0; for (int counter = 0; counter < 67; ++counter) { int64_t startReal = (int64_t)((centerReal - rangeReal * 0.5) * (float)(1 << bits)), startImag = (int64_t)((centerImag + rangeImag * 0.5) * (float)(1 << bits)), incReal = (int64_t)((rangeReal / (float)pixelWidth) * (float)(1 << bits)), incImag = (int64_t)((rangeImag / (float)pixelHeight) * (float)(1 << bits)); uint32_t startTime = millis(); int64_t posImag = startImag; const int16_t pixelHeight2 = pixelHeight / 2 + 1; for (int y = 0; y < pixelHeight2; y++) { yield(); int64_t posReal = startReal; for (int x = 0; x < pixelWidth; x++) { int64_t a = posReal; int64_t b = posImag; int64_t n; for (n = iterations; n > 0 ; n--) { int64_t a2 = (a * a) >> bits; int64_t b2 = (b * b) >> bits; if ((a2 + b2) >= (4 << bits)) break; b = posImag + ((a * b) >> (bits - 1)); a = posReal + a2 - b2; } #if defined(USE_BUFFER) buffer[y * pixelWidth + x] = (n * 29) << 8 | (n * 67); buffer[(pixelHeight - 1 - y) * pixelWidth + x] = (n * 29) << 8 | (n * 67); #else tft.drawPixel(x, y, (n * 29) << 8 | (n * 67)); tft.drawPixel(x, pixelHeight - 1 - y, (n * 29) << 8 | (n * 67)); #endif posReal += incReal; } posImag -= incImag; } #if defined(USE_BUFFER) tft.drawRGBBitmap(0, 0, buffer, pixelWidth, pixelHeight); #endif uint32_t elapsedTime = millis() - startTime; Serial.print("time="); Serial.print(elapsedTime); Serial.print(" ms"); Serial.print(" counter="); Serial.println(counter); if (centerReal > -1.43) centerReal += delta; rangeReal *= 0.8; rangeImag *= 0.8; delta *= 0.9; } } |

The integrated development environment is as important as the
hardware for the success of any project. I choose the Arduino IDE
with the necessary enhancements for ESP8266, ESP32, ILI9341 and
XPT2046. There is no ESP8285 enhancement because the ESP8285 is
software compatible to the ESP8266. Expressif uses the same
firmware - even the build date is 2013 as in the ESP8266. Being a
C programmer since 1987 on Atari ST and a C++ programmer since
1990 on IBM clones, using C/C++ was a no-brainer for me.
The Wifi protocol stack firmware runs always in the ESP. If you
compile your user-program in Arduino-IDE, the firmware is linked
in. At least every 10ms the firmware has to be called. If not, a
watchdog timer interrupt happens. Placing a yield() call at a
convinient position in the search algorithm is all that is needed
to keep the firmware watchdog happy. The watchdog is active even
after the WLAN stack is powered down to save battery power. The
following C source code shows the WiFi switch off on ESP8266 or
ESP8285:
| WiFi.disconnect(); WiFi.mode(WIFI_OFF); WiFi.forceSleepBegin(); yield(); |
In 1915, the Scientific American magazine reported about the mechanical/electromechanical chess automaton from L. Torres y Quevedo. Development started in 1911, presented was the automaton 1914 in Paris. The best part of the article is the description of the algorithm. We can easily implement the algorithm as a software program instead of a hardware automaton. Here is the algorithm:
The algorithm is a simple state machine. The state is position of
white_king, white_rook and black_king. The algorithm transforms
the state into six different non-overlapping cases. These six
cases have some sub-cases which get executed:
1 carries castle to column A,
l' carries the castle to column H,
2 carries the castle downward one square,
3 carries the king downward one square,
4 carries the king one square to the right,
4' carries the king one square to the left,
5 carries the castle one square to the right,
5' carries the castle one square to the left,
6 carries the castle downward one square.
This is really a simple algorithm and I can not imagine a more
simple algorithm. No recursive search, no Megabytes of hash memory
and no Gigahertz of CPU speed needed. For me this is strong
indication for "small is enough". The today available 4-pieces and
5-pieces endgame databases work the same. A simple look-up in
these large data files gives perfect chess play. No thinking
needed, just recall. An opening book allows the best play
according to current knowledge. But new chess knowledge can
invalidate an old opening book. If we ignore this detail, we can
say: playing an opening is recall, too.
The case 1 has a problem. If white_king and white_rock share the
same row, the rock move may be impossible because the king can
block the movement to A column or H column. Therefore we change
the cases into:
1 carries castle to column A if king is not blocking, else next
to the king,
l' carries the castle to column H if king is not blocking, else
next to the king,
And here is the original hardware implementation:
 |
 |
The chessboard is a small square part below the weights in the
left picture.
The normal move generator starts with the from-field and advances
to the to-field. The inverse move generator starts with the
to-field and searches the to-field. Because the move-pattern of
the piece on the from-field is not known, a super-piece
move-pattern is used: the pattern of pawn, knight, bishop and rook
combined. The king-pattern is a one-step bishop/rook pattern and
the queen-pattern is a long-range bishop/rook pattern. The
strongest capture move is the capture of the king. Therefore the
IMG starts with the to-field of the king and goes down the
material ranking (queen, rook, bishop, knight, pawn). The IMG can
search the pieces on the chessboard. The better solution is to
have a pieces-list. The pieces-list has 32 entries for the 32
chess-men. Every piece has its own location. The white knight that
started the game on c1 will remain white_knight1 for the whole
game in the pieces-list. As the game progresses, entries in the
pieces-list will become nil, that is the piece is gone to
chess-heaven. Here is the pieces-list:
| wKg |
wQn |
wRk1 |
wRk2 |
wBp1 |
wBp2 |
wNt1 |
wNt2 |
| wPn1 |
wPn2 | wPn3 | wPn4 | wPn5 | wPn6 | wPn7 | wPn8 |
| bKg |
bQn |
bRk1 |
bRk2 |
bBp1 |
bBp2 |
bNt1 |
bNt2 |
| bPn1 |
bPn2 | bPn3 | bPn4 | bPn5 | bPn6 | bPn7 | bPn8 |
This pieces-list can not handle two queens on the chessboard. If
the opponent gets two queens, the program resigns.
A chess move consists of white piece movement and black piece movement. A ply is a half move. I use ply and bit for singular and plural. I am an engineer. I say 3 Volt and not 3 Volts, because I write 3V and not 3Vs. Because 3Vs means 3*Volt*second for me. But you can do as you like!
The move generator is the oldest part. The Claude Shannon "random
mover" was a move generator and a select a move by chance. Shannon
wrote in 1949: "The writer played a few games against this random
strategy and was able to checkmate generally in four or five moves
(by fool's mate, etc.)". The move generator has the problem of
illegal moves: your king is not allowed to move thru a field that
is under enemy control while doing the castling. Even more simple:
the king is not allowed to move himself into check. The solution
of these problems are: we ignore the castling case.
The king moves himself into check is handled by the search-tree.
In the next ply the tree-search will recognize win, therefore it
will avoid this part of the search-tree. The move generator
produces pseudo-legal moves.
The most simple move generator starts with field a1 and walks
column-first thru the chessboard: a1, a2, a3, ... h8. First
variant is to use a1 ... h8 for white and h8 ... a1 for black.
Second variation is to start in the middle of the chessboard and
go d4, d5, d6, ... d3. Third variant is to go in a spiral: d4, e4,
e5, d5, c5, c4, ... a8. Fourth variant is to use the pieces-list.
You can start with the pawns or you can start with the queen.
Starting with the queen should give more alpha-beta pruning.
Our MG does not generate capture moves. This is the job of the
IMG.
The MG uses a chessboard representation. The most space efficient
is the 8x8
board. A better space/time trade-off has the 10x12
array (mailbox) or the 128 fields 0x88
chessboard. The mirco-Max program used a 129 fields 0x88
chessboard. The last field is to "dump" garbage, thst is to always
have a destination field. I think I stay with the 129 fields 0x88
chessboard.
There is one chessboard and there is one pieces-list. And there
is a search-tree that is 20ply deep. How does this fit together?
We need a move-stack. We have a "do move" operation that executes
the move and pushes the undo-information on the move-stack. And we
have a "undo move" operation that brings the chessboard and
pieces-list back to the previous condition.
The do/undo-move part of the chess program is a nasty piece of
software. It is executed of every search-node, that is hundred
thousand times or even a million times for every move the computer
calculated. Therefore execution shall be quick. But there are
nasty details like undo a castling or undo an en passant
capture or undo a promotion
of a pawn to a queen (queening). Or even the simple question can
the king still do a castling or did he move already e.g. e1-d1-e1?
The good thing is that we can test the do/undo-move very easy.
Even if we need hundreds of test-cases, we should not progress to
advanced topics of our chess program before the do/undo-move is
not rock-solid and fast.
Normally the do/undo-move maintains the material-balance (MB).
Depending of how much chess-knowledge is in the program, the
material-value (MV) of a piece is a constant or a variable. The
traditional values are Pn=1, Nt=Bp=3, Rk=5, Qn=9 and Kg very high,
e.g. Kg=100. This allows 8-bit signed char (int8_t) for the
material balance.
A pawn on seventh row can have the value of a rook. An end game
king and two knights is a draw, an end game with king, knight,
bishop is at least in theory a win. If we have two knights and one
bishop it makes sense to increase the MV of the bishop.
The MB is calculated incrementally. If you loose a pawn, you
subtract the actual pawn value. If the pawn moves to seventh row
and gets the value of a rook, you add the difference of
new_pawn_value and old_pawn_value to the MB.
Like the do/undo-move calculation, the material balance
calculation should be rock-solid and fast.
There is a piece-square table for every kind of chessmen. The
piece-square table "nudges" the balance to good piece positions on
the chessboard. A pawn piece-square table can keep the king shield
intact and suggest a center pawn development before the
development of other pawns. David Kittinger started with "pre scan
heuristics", that is use a chessboard evaluation, the oracle, to
calculate the piece-square tables. In mid game the king should
hide behind the king shield, but in end game the king should go to
the center of the chessboard.
Because the piece-square tables do not change with search depth, a
deep search can cross the mid game to end game "border" and will
have the wrong piece-square table for the deeper search levels.
One possibility is to have two different piece-square tables for
every type of chessmen and "slide" between the tables, that is
give a value of a*table1+(1-a)*table2 with the "sliding" factor a
between 0 or 1.
ESP Schachzwerg will use another algorithm. First the "ESP oracle"
defines the piece-square tables. Then it uses for the first M
searches in the iterative deepening the material balance plus
piece-square tables balance and for the deeper searches only the
material balance. Real material gain is best for ESP Schachzwerg
and can be calculated without piece-square tables balance. The
danger of wrong piece-square tables balance is small for a shallow
search.
The score for depth M search with piece-square tables balence and
for depth N search without piece-square tables balance are stored.
ESP Schachzwerg plays the best move of all. If there is a sure
deep search material gain, e.g. a pawn fork, it will play this,
else it will play the shallow search development move.
The piece-square tables have "nudge" values in centi-pawns. Typical chessmen values in centi-pawns are Pn=100, Nt=320, Bp=330, Rk=500, Qn=900, Kg=20000. A 16-bit signed integer (int16_t) is used for the material balance. Typical piece-pawn tables "nudge" values are -50, ..., -5, 0, 5, ... 50, that is between a 1/20 of a pawn and 1/2 of a pawn.
Usually the do/undo-move maintains the position hash. See
transposition table heuristic for details. The current plan is to
use Zobrist hashing and no assembler programming.
The recursive NegaMax
or NegaScout
algorithm is for many programmers conplicated stuff. The good news
is: We do not need to understand it! We set the piece values,
start the search and get the best move as answer. Okay, for
space-saving we convert the recursive algorithm into an iterative
algorithm and maintain the local program stack-variables in an
indexed struct. And we want to show the principal variation to the
user, that is the chain of ply the computer is most afraid of.
The simple fact that if we have a search depth of 20ply, but we
have a check-mate after 5ply is a special case for the search. But
don't worry. I have seen other programmer's chess program crash,
so why not allow our program to crash, too?
Okay, this is the ugly truth: our search-tree explodes. Even if we
have a branching factor of only 6 because of NegaMax or NegaScout
search, the result is 6^ply. 6^10 is 60 millions, 6^20 is 3656
trillions using the "short scale" trillion.
We get the same position if we start the game with 1. e4 e5, 2.
d4 d5 or if we start with 1. d4 d5 2. e4 e5. This different order
of moves but same position happens over and over in the
search-tree. The transposition
table (TT) helps to avoid duplicated work in the search. But
there are ugly details. The NegaScout algorithm has a start-window
that is not -infinite/+infinite. The TT results are only valid for
"more narrow" start-windows. One solution to this TT problem is to
use NegaMax together with TT.
The "good old" chess computers like the "Mephisto Risc 1MB" from
1992 had 1MByte of TT memory. Our ESP8266 has 80KByte, and we need
2KByte for the do/undo-move and search-tree and XKByte for the
user interface. You want to see nice graphics, yes? The ESP32 is
much better for TT.
The TT is not filled depth-first, but it is filled wide-first. We
want to have all transpositions on depth-1, depth-2, depth-3 until
the TT memory is exhausted. One possibility is that more shallow
transpositions will overwrite deeper transpositions. Another
method is to allow fixed sizes of TT memory for depth-1, depth-2
and so one. In this case there is no need for the individual
transposition to carry the depth information.
The indentification of a position is done with a "hash". Hashing
uniformly distributed data is usualiy done with division
remainder or mod. The chess position is interpreted as a long
number. This long number is divided by an 32-bit prime number. The
remainder is
a good hash.
For me this long division should be done in assembler. Normally a
N bit CPU has a 2*N bit divide by N bit operation with a N bit
quotient and N bit remainder result. Such an operation is normally
not available in C language. It was avaiable in the Forth
language.
Another, less powerful, hash is the Zobrist
hashing. The good thing about this hash is that you can
calculate it incrementally. Like the material-balance you only
have to add or subtract the change on the chessboard.
The disadvantage of hashing are hash collisions.
Because the hash is much smaller than the original data, several
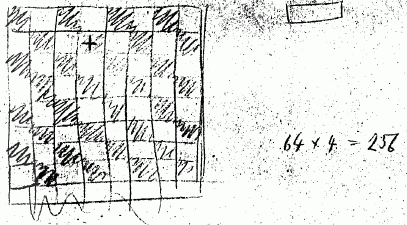
different chess positions have the same hash. Konrad Zuse did a
little calculation in 1941. You need approximate 4 bit (exact
3.7005 bit) to express the 13 separate inhabitants of a field:
wKg, wQn, wRk, wBp, wNt, wPn, bKg, bQn, bRk, bBp, bNt, bPn and
empty. You have 64 fields, that is the information of a chess
position is 64*4bit=256bit. A typical mod-hash is 32-bit long, a
typical Zobrist-hash is 64-bit long. You can imagine how many
hash-collisions are possible! Because of this I call it TT heuristic.
Thank goodness, the chessboard is only sparsely populated. At
least half of the fields are empty. The end game profits most of
TT.
Chess is a game against your opponent and against time. You have
this nasty chess-clock. The iterative
deepening in the chess program helps the computer to stay in
its time budget. If after the ply_N search is done there is time
left, the ply_N+1 search starts. But the iterative deepening does
more. It allows to start the ply_N+1 search with the best ply_N
move. This gives better cut-off or a smaller branching factor. And
there is another advantage. If we have a maximum search of 20 ply,
but we have a mate-in-5, the iterative deepening stops after depth
5. The game is over - at least for the computer. Therefore
iterative deepening makes it unnecessary to report win-in-N or
loose-in-N. The terminate condition for the search is "if there is
no more time or if there is a win". Last but not least does
iterative deepening tell us the size for the transposition table
(TT). After depth_1 search we have used this amount of memory,
after depth_2 we have used that amount of memory and depth_3 TT
can only use the free transposition table memory.
What is the maximum search depth? A chess game can last 80 moves
or 160 ply. But the combinatorial
explosion kills us long time before. We can learn a little
from David Kittinger. Here are some results of some of his chess
computers:
| Year |
Name |
Elo |
max. Ply |
| 1988 |
Novag VIP |
1731 |
20 |
| 1989 |
Novag Super VIP |
1750 |
16 |
| 1995 |
Novag Jade II |
2032 |
16 |
| 1998 |
Novag Turquoise |
2006 |
18 |
Poor David had a handicap. All presented chess computers use the H8 SoC. The H8 SoC has only 1KByte RAM. He could use the RAM for search-depth or for chess-knowledge. In his career he changed first from search-depth to chess-knowledge and later back. Our conclusion: A maximum search-depth between 16 and 20 ply should be fine for ESP Schachzwerg. Lets give the ESP8266 18 ply and the ESP32 20 ply. In 1990 Ed Schröder gave the "Mephisto Polgar 6502 10 MHz" chess computer a maximum search depth of 30 ply. I think this was overkill. The Ed Schröder computer of the following year, "Mephisto Milano 6502 5 MHz", has 22 ply maximum search depth.
Permanent
brain describes the continous working of the chess computer.
While the chess-clock ticks away your time, the chess computer
uses the principal variation, that is the move the chess computer
expects from you, to "think ahead". If you play the expected move,
the chess computer has already perform a ply_N search and can
continue with the ply_N+1 search, that little bastard! If you make
another move than the "feared", the chess computer starts a new
search at ply_0. But this is no problem. You did not play the
strongest move, but a weaker one - at least in the opinion of the
computer. Permanant brain is the holy grail for ESP Schachzwerg.
Hopefully it is not too complicated for my little 1000 Elo natural
brain!
Forward pruning like null move
does reduce the branching factor, but for a price! Even the
forward pruning fans agree on this: "To reduce the chance that
Zugzwang will cause a problem, null move forward pruning is not
done in the end game." A scholar's
mate is a checkmate in the opening. I do not want to forward
prune away something like this. The old chess computer game
comments are full of "why had the program not seen the
checkmate-in-N?". Because the program had forward pruned away the
relevant sub-tree!
I know that debugging do/undo-move, material-balance and Zobrist
hash is hard. I assume that debugging forward pruning is
impossible.
The old mainframe chess programs used 64-bit bitboards. I
do not understand bitboards and I have not heard that the
professional 8-bit chess computer programmers like the Spracklens,
David Kittinger, Ed Schröder, Thomas Nitsche, Elmar Henne, Kaare
Danielson, Richard Lang or Frans Morsch have used bitboards. The
ESP8266 and ESP32 are 32-bit RISC CPUs. But I treat them as
powerful 8-bit CPUs. One important reason for mainframe bitboard
use was that the old-and-ugly beasts could not address space in
chunks of 8-bit. Bitboards are a work-around for mainframe
deficiencies.
For the same odd reason we have "packed
char" in good old Wirth Pascal. On the Control Data
Corporation CDC6000
60-bit word size mainframe, one word could hold one floating point
number or 10 packed 6-bit char. This was the architecture of
Wirth's first Pascal computer and the reason why Pascal is all
capital letters. Or on a 16-bit word machine an unpacked char used
a word (16-bit) and a packed char only 8-bit. By the way: knowing
this makes me really feel old. There is no Wikipedia entry about
"packed char", but the cited Pascal reference book is a newbie
from 1983! I have seen core-memory computers in action like the Siemens
330 or Raytheon
RDS-500 in the system DERD-MC.
And the Telefunken
TR-86 was even older. It had the same small
scale integration technology as the Apollo
guidance computer.
I work as Referent for the german air traffic control. We do our
operational business with Linux operating systems and mostly C/C++
programming. The ops business uses redundant real-time systems
with measured availability of 99.999%, running 24/7 every day of
the year. This is 5 minutes not-planned down-time per year. I have
a hardware background as Fernmeldeelektroniker and a software
background as Diplom Informatiker(FH). I am a ham, too. Callsign
is DL1ADR. This qualifies me as triple nerd™. But I paint with
acrylic colors and I have a big interest in dancing and Kamasutra.
These are my non-nerdy facets. I have three children, two are
already adults. My e-mail address is:
